- Шар вписан в цилиндр площадь полной поверхности
- Что такое вписанный шар в цилиндр?
- Краткая информация о вписанном шаре в цилиндр
- Формула для вычисления объема вписанного шара
- Как вычислить объем вписанного шара в цилиндр?
- Шаг 1: Найти радиус шара
- Шаг 2: Найти высоту цилиндра
- Шаг 3: Вычислить объем шара
- Шаг 4: Вычислить объем цилиндра
- Шаг 5: Вычислить отношение объема шара к объему цилиндра
- Формула для вычисления площади полной поверхности вписанного шара
- Как вычислить площадь полной поверхности вписанного шара в цилиндр?
- Видео:
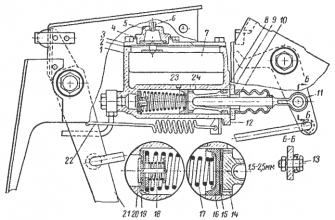
- 12.1. Импульсно-несимметричное смещение центра массы движущегося инерциоида
Шар вписан в цилиндр площадь полной поверхности
В геометрии шар вписывается в цилиндр, когда его диаметр равен высоте цилиндра. Такая конфигурация часто встречается в различных задачах и вычислениях. Формула для определения площади полной поверхности такого шара вписанного в цилиндр может быть полезна при решении задач механики, физики, а также при проектировании различных элементов машин и механизмов.
Для вычисления площади полной поверхности шара вписанного в цилиндр используется следующая формула: S = 2πrh + 2πr^2, где S — площадь полной поверхности, r — радиус шара, h — высота цилиндра.
Одна из задач, в которой нужно знать площадь полной поверхности шара вписанного в цилиндр, это определение объема максимального шара, который можно вписать в данный цилиндр. В этом случае, помимо площади полной поверхности, необходимо также учесть и объем шара.
Что такое вписанный шар в цилиндр?
Вписанный шар в цилиндр — это геометрическая фигура, которая представляет собой шар, целиком находящийся внутри цилиндра таким образом, что шар касается его образующей и двух плоскостей основания. Вписанный шар можно представить себе, как шар, который находится внутри цилиндра таким образом, что его диаметр наибольший.
Для вписанного шара справедливы следующие свойства:
- Центр шара лежит на оси цилиндра и находится на равном расстоянии от плоскостей основания.
- Диаметр шара является диаметром цилиндра.
- Шар касается образующей цилиндра и двух плоскостей основания. Таким образом, его высота равна высоте цилиндра.
Вписанный шар в цилиндр является одним из примеров взаимодействия различных геометрических фигур. Он обладает рядом особенностей и может использоваться в различных задачах и вычислениях.
Краткая информация о вписанном шаре в цилиндр
Вписанный шар — это шар, который полностью помещается внутри другой фигуры без выступания за ее границы. В данном случае речь идет о вписанном шаре в цилиндр.
Чтобы вписать шар в цилиндр, радиус шара должен быть равен радиусу основания цилиндра. Его диаметр совпадает с диаметром цилиндра и проходит через его центр.
Вписанный шар в цилиндр образует особую геометрическую фигуру, обладающую рядом интересных свойств:
- Центр вписанного шара совпадает с центром цилиндра.
- Диаметр вписанного шара равен диаметру цилиндра.
- Высота цилиндра является суммой диаметра вписанного шара и высоты взятого с центром в шар, проходящим через цилиндр.
Также можно вычислить площадь полной поверхности вписанного шара в цилиндр по формуле:
Sполн. пов. = 2πr2 + 2πrh
где Sполн. пов. — площадь полной поверхности вписанного шара, r — радиус шара, h — высота цилиндра.
Формула для вычисления объема вписанного шара
Объем вписанного шара в цилиндр может быть вычислен по следующей формуле:
| Формула: | V = 4/3 * π * r3 |
Где:
- V — объем вписанного шара
- π — математическая константа, приближенно равная 3.14159
- r — радиус шара
Данная формула основана на концепции вписанного шара, который полностью помещается внутри цилиндра так, что его диаметр равен диаметру основания цилиндра. Объем шара зависит от его радиуса, и формула позволяет измерить этот объем.
Как вычислить объем вписанного шара в цилиндр?
Для вычисления объема вписанного шара в цилиндр существуют несколько способов. Один из них заключается в использовании формулы объема шара и формулы объема цилиндра.
Шаг 1: Найти радиус шара
Первым шагом необходимо найти радиус шара, который является половиной диаметра. Радиус шара может быть известен, либо его можно найти, зная диаметр или длину его окружности. Если радиус шара уже известен, пропустите этот шаг и перейдите к следующему.
Шаг 2: Найти высоту цилиндра
Далее необходимо найти высоту цилиндра, в который вписан шар. Высота цилиндра может быть известна, либо ее можно найти, зная радиус основания цилиндра и его объем. Если высота цилиндра уже известна, пропустите этот шаг и перейдите к следующему.
Шаг 3: Вычислить объем шара
После получения значения радиуса шара и высоты цилиндра можно вычислить объем шара. Формула для вычисления объема шара:
- Найдите радиус шара.
- Воспользуйтесь формулой $\frac{4}{3}\pi r^3$, где $r$ — радиус шара.
- Вычислите значение данного выражения.
Шаг 4: Вычислить объем цилиндра
После вычисления объема шара можно перейти к вычислению объема цилиндра, в который вписан данный шар. Формула для вычисления объема цилиндра:
- Найдите радиус цилиндра.
- Найдите высоту цилиндра.
- Воспользуйтесь формулой $\pi r^2h$, где $r$ — радиус цилиндра, $h$ — высота цилиндра.
- Вычислите значение данного выражения.
Шаг 5: Вычислить отношение объема шара к объему цилиндра
После вычисления объема шара и объема цилиндра можно вычислить отношение объема шара к объему цилиндра, чтобы узнать, насколько шар заполняет пространство внутри цилиндра. Для этого необходимо разделить объем шара на объем цилиндра и умножить результат на 100%, чтобы получить процентное значение.
- Вычислите отношение $\frac{V_{\text{шара}}}{V_{\text{цилиндра}}}$, где $V_{\text{шара}}$ — объем шара, $V_{\text{цилиндра}}$ — объем цилиндра.
- Умножьте результат на 100%.
- Получите процентное значение отношения.
Таким образом, можно вычислить объем вписанного шара в цилиндр, а также узнать, насколько шар заполняет пространство внутри цилиндра.
Формула для вычисления площади полной поверхности вписанного шара
При рассмотрении шара, вписанного в цилиндр, мы можем вычислить его площадь полной поверхности. Площадь полной поверхности вписанного шара является суммой площади внешней поверхности шара и площади боковой поверхности цилиндра.
Формула для вычисления площади полной поверхности вписанного шара можно записать следующим образом:
| Площадь полной поверхности шара | : | 4πr² |
| Площадь боковой поверхности цилиндра | : | 2πrh |
Где r — радиус шара, а h — высота цилиндра.
Итак, чтобы вычислить площадь полной поверхности вписанного шара, необходимо знать его радиус и высоту цилиндра.
Как вычислить площадь полной поверхности вписанного шара в цилиндр?
Площадь полной поверхности вписанного шара в цилиндр можно вычислить с использованием формулы. Для расчета необходимо знать радиус и высоту цилиндра.
Шаги для вычисления площади полной поверхности вписанного шара в цилиндр:
- Найти площадь боковой поверхности цилиндра, используя формулу: Sб = 2πrh, где r — радиус цилиндра, h — высота цилиндра.
- Найти площадь основания цилиндра, используя формулу: Sосн = πr^2, где r — радиус цилиндра.
- Найти площадь полной поверхности цилиндра, складывая площадь боковой поверхности и площадь основания: Stот = Sб + 2Sосн.
- Найти площадь полной поверхности вписанного шара, используя формулу: Stши = 4πr^2, где r — радиус цилиндра.
Теперь, зная площадь полной поверхности цилиндра и площадь полной поверхности вписанного шара, можно вычислить площадь, которая закрыта поверхностью шара внутри цилиндра. Для этого необходимо вычесть площадь поверхности шара из площади поверхности цилиндра: Sзакр = Stот — Stши.
Таким образом, мы получим площадь полной поверхности вписанного шара в цилиндр.
Видео:
12.1. Импульсно-несимметричное смещение центра массы движущегося инерциоида
12.1. Импульсно-несимметричное смещение центра массы движущегося инерциоида by Denis Permyakov 19 hours ago 2 hours, 28 minutes 676 views