Как называется цилиндр с разными диаметрами оснований

Цилиндр – это геометрическое тело, образованное при вращении прямоугольника вокруг его стороны. Основания цилиндра являются кругами, а его боковая поверхность представляет собой равнобедренную трапецию. Существуют различные типы цилиндров, отличающиеся размерами и формой оснований.

Одним из интересных типов цилиндров является цилиндр с разными диаметрами оснований. В данном случае, диаметры оснований не совпадают, что придает цилиндру особую форму и свойства.

Цилиндр с разными диаметрами оснований применяется в различных областях, например, в архитектуре и инженерии. Его основания могут иметь разные размеры и формы, что позволяет создать уникальные конструкции и сооружения. Благодаря своей форме, цилиндр с разными диаметрами оснований обладает высокой устойчивостью и прочностью.

Цилиндр с разными диаметрами оснований – это уникальная геометрическая фигура, которая привлекает внимание своей необычной формой и является важным элементом в различных областях человеческой деятельности.

Название и структура

Цилиндр с разными диаметрами оснований – геометрическое тело, состоящее из двух различных по размеру круглых оснований, соединенных цилиндрической поверхностью. Основания цилиндра представляют собой круги, диаметры которых могут отличаться друг от друга.

Цилиндр с разными диаметрами оснований имеет следующую структуру:

1. Верхнее основание – это круг с большим диаметром, расположенный сверху.
2. Нижнее основание – это круг с меньшим диаметром, помещенный внизу.
3. Цилиндрическая поверхность соединяет верхнее и нижнее основания и представляет собой бесконечное количество прямоугольников, высота каждого из которых равна высоте цилиндра и ширина равна длине окружности одного из оснований.

Структура цилиндра с разными диаметрами оснований позволяет определить его объем и площадь поверхности:

• Объем цилиндра с разными диаметрами оснований равен произведению площади верхнего основания на высоту цилиндра. Формула для расчета объема: V = π * R^2 * h, где π — математическая константа (примерно равна 3.14), R – радиус верхнего основания, h – высота цилиндра.
• Площадь поверхности цилиндра с разными диаметрами оснований состоит из площадей боковой поверхности и двух оснований. Формула для расчета площади поверхности: S = 2πR * h + 2πR1^2, где R1 – радиус нижнего основания.

Известные свойства цилиндра с разными диаметрами оснований позволяют использовать его в различных областях, таких как архитектура, инженерия, математика, графика и т. д.

Особенности и применение

Особенности цилиндра с разными диаметрами оснований

Цилиндр с разными диаметрами оснований представляет собой геометрическую фигуру, у которой основания отличаются по размеру. В отличие от цилиндра с одинаковыми диаметрами оснований, у такого цилиндра боковая поверхность является треугольником. Благодаря этой особенности, цилиндр с разными диаметрами оснований обладает рядом уникальных свойств и применений.

Применение цилиндра с разными диаметрами оснований

Цилиндр с разными диаметрами оснований широко применяется в различных областях науки и техники. Вот некоторые из них:

• Машиностроение: В промышленности цилиндры с разными диаметрами оснований используются для создания гидравлических систем, пневматических тормозных систем, гидроцилиндров и других устройств, требующих преобразования энергии.
• Архитектура: Цилиндры с разными диаметрами оснований могут использоваться в архитектуре для создания оригинальных и необычных форм зданий или сооружений.
• Медицина: В медицинской практике цилиндры с разными диаметрами оснований могут использоваться для создания протезов и имплантатов, а также для моделирования различных органов и тканей человека в научно-исследовательских целях.
• Математика и физика: Цилиндры с разными диаметрами оснований являются объектами исследования в математике и физике, позволяя изучать такие аспекты, как объем, площадь поверхности, центр масс и другие характеристики.

Цилиндр с разными диаметрами оснований объединяет в себе уникальные свойства и может быть использован во множестве областей. Его геометрическая форма позволяет реализовывать разнообразные идеи и решать сложные задачи в различных областях деятельности.

Расчет объема и площади поверхности

Расчет объема и площади поверхности цилиндра с разными диаметрами оснований выполняется по формулам, которые зависят от параметров цилиндра: радиуса одного из оснований, радиуса второго основания и высоты цилиндра.

Объем цилиндра

Объем цилиндра вычисляется по следующей формуле:

V =

π

r12 + r22

h

:

4

где:

• V — объем цилиндра;
• π — число пи (примерно равное 3,14159);
• r₁ — радиус одного из оснований;
• r₂ — радиус второго основания;
• h — высота цилиндра.

Площадь поверхности цилиндра

Площадь поверхности цилиндра состоит из площади двух оснований и площади боковой поверхности и вычисляется по следующей формуле:

S =	2πr12 + 2πr1r2

где:

• S — площадь поверхности цилиндра;
• π — число пи (примерно равное 3,14159);
• r₁ — радиус одного из оснований;
• r₂ — радиус второго основания.

Математические формулы и свойства

1. Формула объема цилиндра

Объем цилиндра можно вычислить, используя следующую формулу:

V = S × h,

где V — объем цилиндра,

S — площадь основания,

h — высота цилиндра.

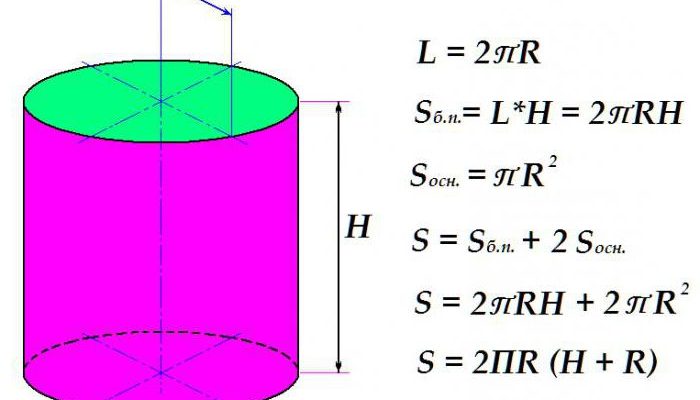
2. Формула площади боковой поверхности цилиндра

Площадь боковой поверхности цилиндра можно вычислить, используя следующую формулу:

Sб = 2πr × h,

где Sб — площадь боковой поверхности цилиндра,

r — радиус основания цилиндра,

h — высота цилиндра.

3. Формула полной поверхности цилиндра

Полная поверхность цилиндра можно вычислить, используя следующую формулу:

Sп = 2πr² + 2πr × h,

где Sп — полная поверхность цилиндра,

r — радиус основания цилиндра,

h — высота цилиндра.

4. Свойства цилиндра

1. Цилиндр имеет два основания, которые являются плоскими и круглыми.
2. Высота цилиндра — это расстояние между основаниями, проведенное вдоль оси.
3. Цилиндр имеет форму, близкую к прямоугольной.
4. Боковая поверхность цилиндра представляет собой цилиндрическую поверхность, которая состоит из всех точек, лежащих между двумя основаниями.
5. Цилиндр обладает острым/тупым углом между основаниями, в зависимости от соотношения диаметров оснований.

Примеры и задачи

Пример 1:

Найдите площадь поверхности и объем цилиндра, если радиусы его оснований равны 3 см и 6 см, а высота равна 8 см.

Решение:

Площадь поверхности цилиндра вычисляется по формуле:

S = 2πr₁h + 2πr₂h + πr₁² + πr₂²

где S — площадь поверхности цилиндра, π — математическая константа, примерное значение которой равно 3.1416, r₁ и r₂ — радиусы оснований цилиндра, h — высота цилиндра.

Подставим значения в формулу:

S = 2 * 3.1416 * 3 * 8 + 2 * 3.1416 * 6 * 8 + 3.1416 * 3² + 3.1416 * 6²

S ≈ 150.7968 + 301.5936 + 28.2744 + 113.0976 ≈ 593.7624 см²

Ответ: площадь поверхности цилиндра примерно равна 593.7624 см².

Объем цилиндра вычисляется по формуле:

V = π(r₁² + r₂²)h

где V — объем цилиндра, π — математическая константа, примерное значение которой равно 3.1416, r₁ и r₂ — радиусы оснований цилиндра, h — высота цилиндра.

Подставим значения в формулу:

V = 3.1416 * (3² + 6²) * 8

V = 3.1416 * (9 + 36) * 8

V ≈ 3.1416 * 45 * 8 ≈ 1130.9736 см³

Ответ: объем цилиндра примерно равен 1130.9736 см³.

Пример 2:

Найдите площадь поверхности и объем цилиндра, если радиус основания равен 5 см, а высота равна 10 см.

Решение:

Площадь поверхности цилиндра вычисляется по формуле:

S = 2πrh + 2πr²

где S — площадь поверхности цилиндра, π — математическая константа, примерное значение которой равно 3.1416, r — радиус основания цилиндра, h — высота цилиндра.

Подставим значения в формулу:

S = 2 * 3.1416 * 5 * 10 + 2 * 3.1416 * 5²

S = 3.1416 * 100 + 3.1416 * 25

S ≈ 314.16 + 78.54 ≈ 392.70 см²

Ответ: площадь поверхности цилиндра примерно равна 392.70 см².

Объем цилиндра вычисляется по формуле:

V = πr²h

где V — объем цилиндра, π — математическая константа, примерное значение которой равно 3.1416, r — радиус основания цилиндра, h — высота цилиндра.

Подставим значения в формулу:

V = 3.1416 * 5² * 10

V = 3.1416 * 25 * 10

V ≈ 3.1416 * 250 ≈ 785.4 см³

Ответ: объем цилиндра примерно равен 785.4 см³.

Видео:

Объем цилиндра. Практическая часть. 11 класс.

Объем цилиндра. Практическая часть. 11 класс. by МЕКТЕП OnLine ГЕОМЕТРИЯ 6 months ago 7 minutes, 23 seconds 698 views